Примеры решений задач по теории игр
Теория игр для чайников
В этом разделе вы найдете бесплатные примеры решений задач по теории игр: нахождение нижней и верхней цены игры, седловой точки, решение игр аналитическим и графическим методом, решение игр сведением к задачам ЛП, решение игр с природой по различным критериям и т.д.
Трудности с задачами? МатБюро поможет: контрольные по теории игр.
Решения матричных игр онлайн
Задача 1. Зная платежную матрицу
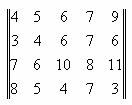
определить нижнюю и верхнюю цены игры и найти решение матричной игры.
Задача 2. Найти стратегии игроков А, В и цену игры, заданной матрицей (с помощью формул и графически)
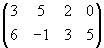
Задача 3. Найти оптимальный вариант электростанции по критериям Лапласа, Вальда, Гурвица с показателями 0,8 и 0,3 и Сэвиджа по заданной таблице эффективностей (Таблица эффективностей в файле).
Задача 4. Швейное предприятие реализуется свою продукцию через магазин. Сбыт зависит от состояния погоды. В условиях теплой погоды предприятие реализует 1000 костюмов и 2300 платьев, а при прохладной погоде - 1400 костюмов и 700 платьев. Затраты на изготовление одного костюма равны 20, а платья - 5 рублям, цена реализации соответственно равна 40 рублей и 12 рублей. Определить оптимальную стратегию предприятия.
Задача 5. Найти решение и цену игры, заданной следующей платежной матрицей: $$A=\left( \begin{array} \\12& 22\\ 32 &2 \end{array} \right)$$
Задача 6. Выполните доминирование и найдите оптимальное решение и цену игры, заданной матрицей. $$A=\left( \begin{array} \\1& 2 & 1 & 2\\ 2& 1& 2& 4\\ 3& 3& 2& 2\\ 4& 1& 3& 3\\ \end{array} \right)$$
Задача 7. Дана матрица игры. Привести игру к задаче линейного программирования. Найти решение матричной игры в смешанных стратегиях $$A=\left( \begin{array}\\ 2& 4 & 8& 5\\ 6& 2& 4& 6\\ 3& 2& 5& 4\\ \end{array} \right)$$



